Understanding how to solve quadratic equations is crucial because of the importance of these equations in mathematics. 4x ^ 2 – 5x – 12 = 0 Let’s examine and dissect the equation 4×2 – 5x – 12 = 0 in more detail. We must first identify the coefficients. The constant term has a value of -12, the coefficient of x is -5, and the coefficient of x 2 is 4. 4x ^ 2 – 5x – 12 = 0. Applying the quadratic formula, we can find the solutions for x. By plugging in the values, we can calculate the answers and determine the values of x that satisfy the equation.
Understanding Quadratic Equations: A Key to Solving Complex Problems
Quadratic equations are fundamental mathematical expressions in various fields, from physics and engineering to finance and computer science. A solid understanding of quadratic equations is crucial for effectively tackling complex problems.
A quadratic equation is a second-degree polynomial equation in which the highest power of the variable is 2. Its general form is ax^2 + bx + c = 0, where a, b, and c are constants, and x represents the variable. The solutions to quadratic equations are often referred to as roots or solutions.
The graph of a quadratic equation is a parabola with a symmetric U-shape. This visual representation helps us grasp the behavior and properties of quadratic equations.
One key concept in understanding quadratic equations is the discriminant, denoted as Δ (delta). The discriminant, given by the expression b^2 – 4ac, helps determine the nature of the roots if Δ > 0, the equation has two distinct real roots. When Δ = 0, there is one fundamental, repeated root. And if Δ < 0, the equation has no real roots but possesses two complex sources.
Solving quadratic equations involves various techniques, including factoring, completing the square, and using the quadratic formula. These methods allow us to find the values of x that satisfy the equation and help us solve real-world problems efficiently.
By comprehending the underlying principles and techniques of quadratic equations, individuals can enhance their problem-solving skills and unlock new possibilities in mathematics and other fields of study.
Identifying the Coefficients: Unveiling the Building Blocks of Equations
When working with mathematical equations, one of the initial steps is identifying the coefficients. Coefficients are the numerical values multiplied by variables in an equation, providing crucial information about the relationship between variables and constants.
In a general form, a polynomial equation can be expressed as ax^n + bx^(n-1) + … + cx + d = 0, where a, b, c, and d are coefficients, x represents the variable, and n is the degree of the equation. Focusing on quadratic equations specifically, the highest power of x is 2, making it easier to identify the coefficients.
Consider an example equation: 4x^2 – 5x – 12 = 0. Here, the coefficient of x^2 is 4, which tells us that the term 4x^2 is four times larger than x^2 alone. Similarly, the coefficient of x is -5, indicating that the time -5x is multiplied by -5.
Identifying the coefficients enables us to manipulate and solve equations more effectively. Whether we use factoring, completing the square, or the quadratic formula, understanding the coefficients is vital for applying the appropriate technique and finding solutions accurately.
You Can Read This Simler Article: 27″ Iiyama G-Master GB2760HSU-B1
By honing our skills in identifying coefficients, we gain a deeper comprehension of the structure and behavior of equations. This knowledge empowers us to confidently tackle a wide range of mathematical problems, paving the way for success in various academic and practical endeavors.
Applying the Quadratic Formula: Unlocking Solutions to Quadratic Equations
The quadratic formula is a powerful tool for solving quadratic equations of ax^2 + bx + c = 0. Applying the quadratic formula can provide precise solutions when faced with such equations. The procedure is x = (-b ± √(b^2 – 4ac)) / (2a), where a, b, and c are the coefficients of the equation. By plugging in the values and simplifying the equation, we can calculate the values of x that satisfy the quadratic equation. This technique enables us to solve complex mathematical problems and accurately uncover the roots of quadratic equations.
Finding the Solutions: Unveiling Answers to Quadratic Equations
Finding the solutions to quadratic equations is an essential skill in mathematics, enabling us to solve many problems. Whether we encounter quadratic equations in algebra, physics, or engineering, understanding how to find the solutions is crucial for determining unknown values.
Quadratic equations, in the form of ax^2 + bx + c = 0, can be solved using various methods, with one standard approach being the quadratic formula. The quadratic formula provides a systematic way to find the solutions for x, regardless of the values of a, b, and c. By substituting the coefficients into the formula and simplifying the equation, we can determine the values of x that satisfy the quadratic equation.
The solutions to quadratic equations can take different forms. In some cases, the equation yields two distinct real solutions. These solutions represent the x-values at which the quadratic equation intersects the x-axis. Other times, the equation produces a single real solution, indicating that the quadratic equation touches the x-axis at one point. Additionally, quadratic equations can result in complex solutions involving the imaginary unit (√-1).
By diligently applying techniques like the quadratic formula, we can navigate the complexities of quadratic equations and find solutions. This skill extends beyond mathematics, enhancing problem-solving abilities and promoting logical thinking. Understanding how to find the answers empowers us to unravel the mysteries hidden within quadratic equations and confidently tackle real-world challenges.
Also, Read The Following: 150 USD to CAD

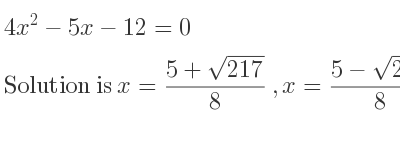









Discussion about this post